About SileX
The course mechanisme design II applies the previously acquired knowledge about flexure mechanisms in a concrete project. The goal was to design a mechanisme fulfilling specifications of a real world application. I worked on this project with four team Members: Nathalie Künzle, Andi Piatoni, Mariem Oulare, and Océane Mauroux.
The Problem
One of the major technologies in micro manufacturing is femtosecond laser fabrication using short laser bursts to erode matter. The technology is limited by the speed with which the laser can be displaced relative to the material. The project SileX developes a mechanisme with two degrees of freedom in rotation to maximize the mirror displacement and hence manufacturing speed.
Requirements
no more than 1.5 micro parasitic motion of the laser spot
At least 1.5 degrees of rotation with a precision of 0.015 degrees
Maximal average force of the actuators 1.8N (RMS)
Maximal Manufacturing costs of 20k
Frequency of at least 860 Hz
The Solution
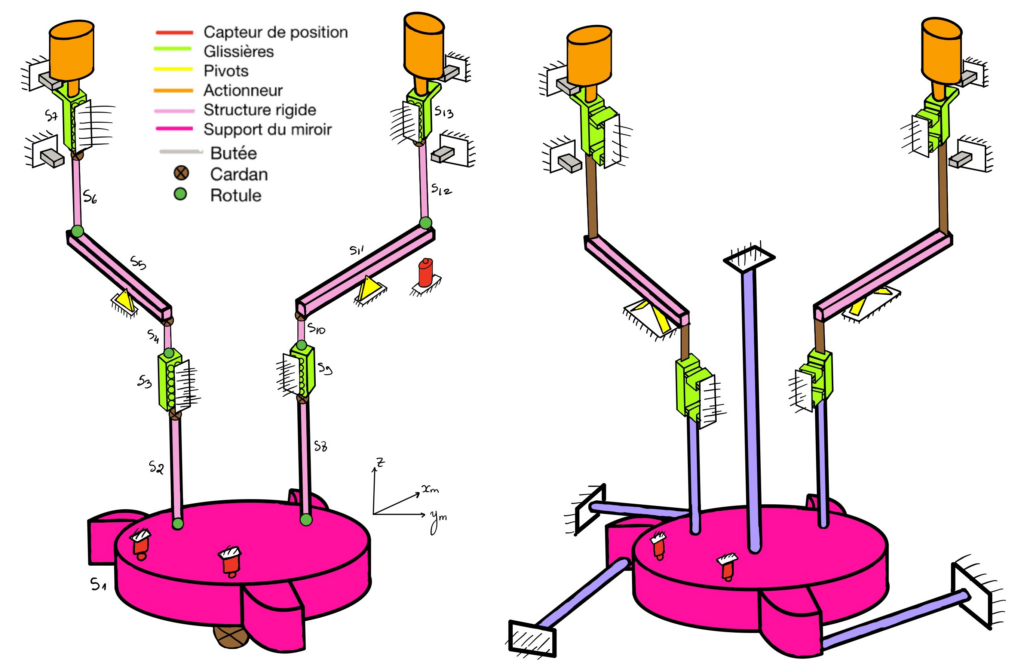
- The mirror joint blocks translation in x,y, and z and z-rotation using four rods.
- The dynamic equilibrium system (horizontal purple bars) compensates the moment created by the mirror. Together with the symmetric connections, they avoid any creation of forces to the fixing structure.
- The connections are guided by parallelogram flexure mechanisms.
- Two actuators independently control the x and y rotation. The spring constant of the mechanism is sufficiently low to allow the actuators to oscillate at about 1kHz
- Two sensors measure the rotation of the mirror to form a closed feedback loop with the actuators. They are placed sufficiently far away from the center of rotation to guarantee a sufficient resolution.
More details about the principle and design choices can be found in the report.
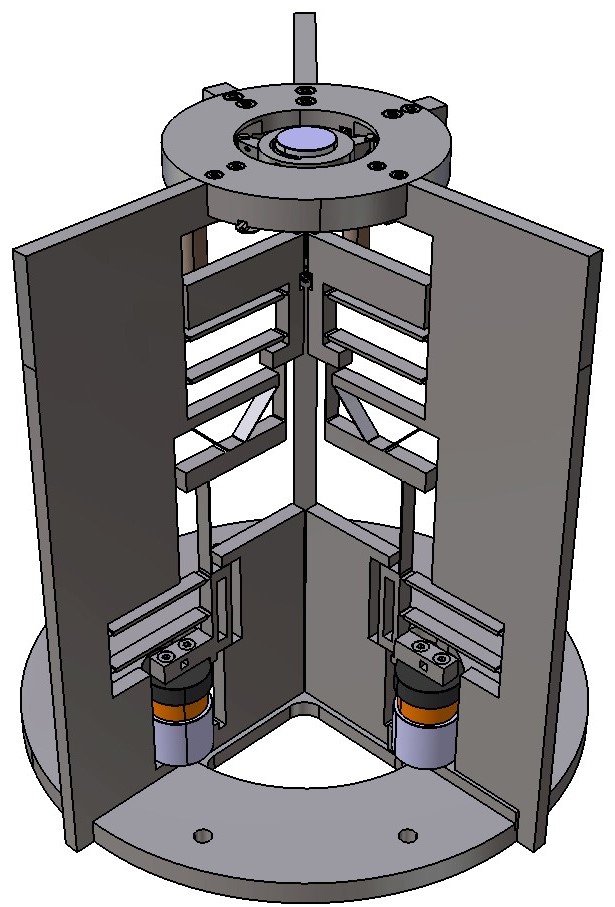
The Path to the Solution
We developed and evaluated a total of five mechanisms before committing to the final solution shown above. This is a merge of three previously studied solutions optimizing the dynamic equilibrium and parasitic motion. I mostly worked on the calculations for the dynamic equilibrium
After choosing the form of the mechanism we had to dimension it to maximize the frequency of oscillation. For this, I wrote a MatLab model of our system connecting all the relevant geometrical parameters to the oscillation frequency. Adding constraints like minimal and maximal dimensions, buckling avoidance , and dymanic equlibrium resulted in a constrained optimization problem.
I expected to to run the program and directly get the optimal solution. However, reality proved me wrong. The two major problems were the non-convexity and the sensitivity to rounding errors due to the different order of magnitude of the parameters. I solved this problem by reducing most of the equations by hand and reducing the number of variables. After many hours and different starting points we finally had a solution that fulfilled all the constraints and was most likely (at least close to) optimal.
Finally, we implemented the solution of the optimization problem in a 3d model. As wer previously included dimensinal constraints this step created only minor problems that could easily be solved. We then successfully checked the dynamics and parasitic motion in a finite element simulation. The simulation slightly differed from our theoretical calculations but still fulfilled all the requirements.
We 3D printed our model with some minor adjustments to consider the different mechanical properties of polymers and metal to ensure the mechanical integrity and feasibility of our design. Manufacturing the mechanism with its original materials was sadly not possible due to the associated costs.
Lessons Learned
This project was an amazing opportunity to apply and deepen previously acquired knowledge about mechanism analysis and design. It gave me the opportunity to take all the major design steps from specifications to a 3D printed prototype.
Additionally, I learned about solving constrained optimization problems with MatLab and potential problems.